Asymptotic Notation

Last updated on July 13th, 2024 at 11:03 am

We’ll discuss types of asymptotic notation, types of notation – theta, big-O, omega, small-o, and small omega notation, the growth rate of an algorithm, analysis of loops – calculation of runtime complexity, and growth of function.

1. What is Asymptotic Notation?

Asymptotic notation is used to determine rough estimates of the relative running time of algorithms. It is based on two assumptions, which hold in most of the cases and have their importance.

It is very important to understand the assumptions and limitations of asymptotic notations:

1. Input Size: how the running time of an algorithm grows for a large input size n
2. Constant: The running time of an algorithm also depends on various constants. But for a large input n, the constant factors would be ignored

Example:

a <- 0	1 unit	1 time
for i <- 1 to n do{	1 unit	n times
for j <- 1 to n do{	1 unit	n(n+1)/2 times
a <- a+1	1 unit	n(n+1)/2 times

1.1 Theta Notation(Θ-notation)

Theta notation shows the tightest upper bound and the tightest lower bound to the given function. It is used to define the average-case running time.

Big-Theta of g(n), written as f(n) = Θ(g(n))

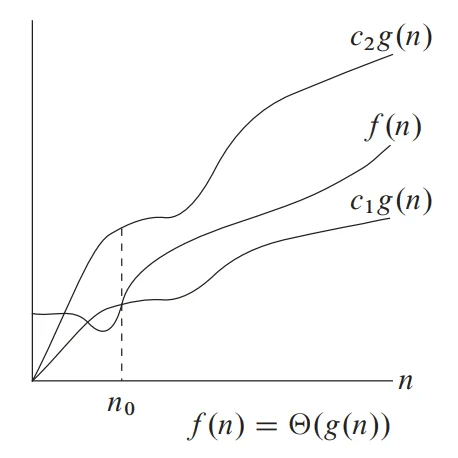
In average case analysis, we take all possible inputs and calculate computing time for all of its inputs.

1.2 Big-O Notation (O-notation)

Big-O notation shows the upper bound to the given function. It measures the worst-case time complexity.

Big-O of g(n), written as f(n) = O(g(n))

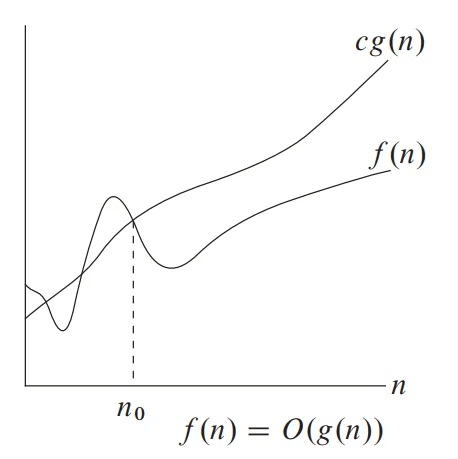
In the best-case analysis, we calculate lower bound on running time of an algorithm.

1.3 Omega Notation (Ω-notation)

Omega notation shows the lower bound to the given function. It measures the best-case time complexity.

Big-Omega of g(n), written as f(n) = Ω(g(n))

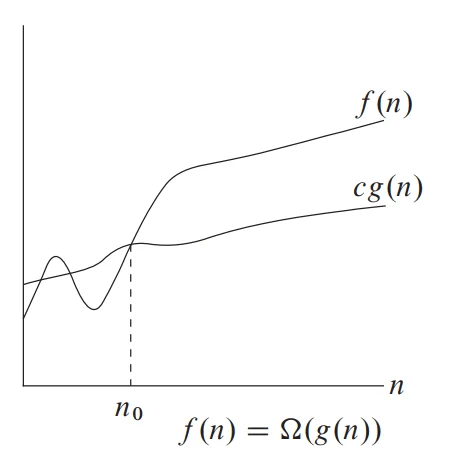
In the best-case analysis, we calculate lower bound on running time of an algorithm

1.4 Small-o Notation (o-notation)

Small-o represents an upper bound which is not a tight upper bound. It is also used to define the worst-case running time

1.5 Small Omega Notation (ω-notation)

Small omega (ω) represents a lower bound which is not a tight lower bound. It is used to define the best-case running time.

Lower Bound <= Average Time <= Upper Bound

2. Types of Complexities

• Constant time complexity: O(1)
• Logarithmic time complexity: O(log(log n)), O(√log )and O(log n)
• Linear time complexity: O(√n) and O(n)
• Polynomial time complexity: O(n^k), where k is a constant and is >1
• Exponential time complexity: O(aⁿ), where a > 1

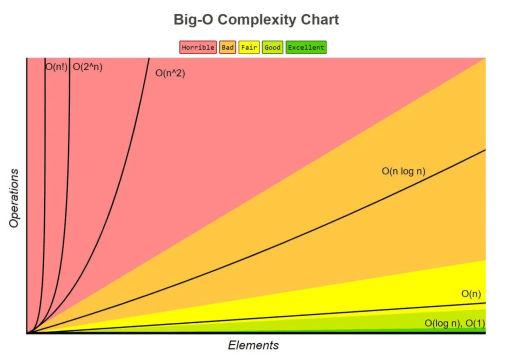
3. Growth Rate of Algorithm

Growth Rate of Algorithm is the rate at which the running time increases as a function of input.

log(n!) < (log(n))!

log(log*n) < log*(log n)

n < (log n)^{log n}

2ⁿ < n! < nⁿ

3.1 List of the growth rate of an algorithm:

Time Complexity	Name	Example
O(1)	Constant	Adding an element to the front of a linked list
O(log n)	Logarithmic	Finding an element in a sorted array
O(n)	Linear	Finding an element in an unsorted array
O(n log n)	Linear logarithmic	Sorting n items by ‘divide-and-conquer’
O(n2)	Quadratic	Shortest path between two nodes in a graph
O(n3)	Cubic	Matrix Multiplication
O(2n)	Exponential	The Tower of Hanoi

4. Analysis Of Loops

4.1 O(1) – Constant

Time complexity of a function (or set of statements) is O(1). It doesn’t contain a loop, recursion, or call to any other non-constant time function.

// Here c is a constant
for (int i=1; i<=c; i++)
{
  //some O(1) expressions
}

4.2 O(n) – Linear

Time Complexity of a loop is O(n) if the loop variables are incremented/decremented by a constant value.

// Here c is a positive integer constant
for (int i=1; i<=n; i+=c)
{
  //some O(1) expressions
}
for (int i=n; i>0; i-=c)
{
  //some O(1) expressions
}

4.4 O(n^c) – Exponential

Time Complexity of nested loops is O(n^c) if the number of times the innermost statement is executed.

Selection Sort and Insertion Sort have O(n²) time complexity.

for (int i=1; i<=n; i+=c)
{
  for (int j=1; j<=n; j+=c)
    {
      //some O(1) expressions
    }
  }
  for (int i=n; i>0; i+=c)
  {
  for (int j=i+1; j<=n; j+=c)
  {
    //some O(1) expressions
  }
}

4.3 O(log n) – Logarithmic

Time Complexity of a loop is O(log n) if loop variables are divided/multiplied by a constant value.

main()
{
  i=1;
  while (i<n)
  {
    i=2*i;
  }
}

5. Growth of Functions

The order of growth of the running time of an algorithm gives a simple characterization of the algorithm’s efficiency.

The decreasing order of growth of time complexity is:

2²ⁿ > n! > 4ⁿ > 2ⁿ > n² > n(log n) > log(n!) > n > 2^{log n} > log² n > √log n > log(log n) >1

FAQs