Linear Search Algorithm

Last updated on July 13th, 2024 at 11:10 am

We will discuss the Linear Search Algorithm, pseudo code, Code implementation of Linear Search in C, C++, Java, JavaScript, Python, advantages & disadvantages, and time & space complexity of Linear Search.

1. What is Linear Search?

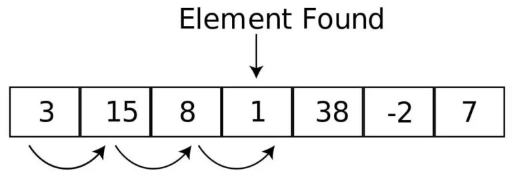
Linear search is a sequential way of finding an element in a given list. Linear search is a special case of brute force search. Its worst case is proportional to the number of elements in the list.

In Linear Search, we start from one end and check every element until the desired element is not found.

1.1 Pseudocode for Linear Search

LINEAR_SEARCH (A[ ], x) 
1. i = 1 
2. while (A[i] = = x and i < n)
3. i = i + 1 
4. if (A[i] = = x) 
5. return i else r
6. return 0

2. Implementation of Linear Search Algorithm

2.1 Linear Search Algorithm in C

#include <stdio.h>

int linearSearch(int arr[], int n, int x) {
    for (int i = 0; i < n; i++) {
        if (arr[i] == x) {
            return i; // If element is found, return its index
        }
    }
    return -1; // If element is not found, return -1
}

int main() {
    int arr[] = {2, 3, 4, 10, 40};
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 10;
    int result = linearSearch(arr, n, x);
    if (result == -1) {
        printf("Element is not present in array\n");
    } else {
        printf("Element is present at index %d\n", result);
    }
    return 0;
}

2.1.1 Code Explanation of Linear Search

• linearSearch function takes an array arr[], its size n, and the element to be searched x.
• The function iterates through the array using a for loop.
• Inside the loop, it checks if the current element is equal to x. If found, it returns the index of that element.
• If the element is not found after iterating through the entire array, it returns -1.
• In the main function, an array arr[] is defined along with its size n and the element to be searched x.
• The linearSearch function is called, and the result is printed.

2.2 Linear Search Algorithm in C++

#include <iostream>
#include <vector>

int linearSearch(std::vector<int>& arr, int x) {
    for (int i = 0; i < arr.size(); i++) {
        if (arr[i] == x) {
            return i; // If element is found, return its index
        }
    }
    return -1; // If element is not found, return -1
}

int main() {
    std::vector<int> arr = {2, 3, 4, 10, 40};
    int x = 10;
    int result = linearSearch(arr, x);
    if (result == -1) {
        std::cout << "Element is not present in array" << std::endl;
    } else {
        std::cout << "Element is present at index " << result << std::endl;
    }
    return 0;
}

2.3 Linear Search Algorithm in Java

public class LinearSearch {
    public static int linearSearch(int[] arr, int x) {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == x) {
                return i; // If element is found, return its index
            }
        }
        return -1; // If element is not found, return -1
    }

    public static void main(String[] args) {
        int[] arr = {2, 3, 4, 10, 40};
        int x = 10;
        int result = linearSearch(arr, x);
        if (result == -1) {
            System.out.println("Element is not present in array");
        } else {
            System.out.println("Element is present at index " + result);
        }
    }
}

2.4 Linear Search Algorithm in JavaScript

function linearSearch(arr, x) {
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] === x) {
            return i; // If element is found, return its index
        }
    }
    return -1; // If element is not found, return -1
}

let arr = [2, 3, 4, 10, 40];
let x = 10;
let result = linearSearch(arr, x);
if (result === -1) {
    console.log("Element is not present in array");
} else {
    console.log("Element is present at index " + result);
}

2.5 Linear Search Algorithm in Python

def linear_search(arr, x):
    for i in range(len(arr)):
        if arr[i] == x:
            return i  # If element is found, return its index
    return -1  # If element is not found, return -1

arr = [2, 3, 4, 10, 40]
x = 10
result = linear_search(arr, x)
if result == -1:
    print("Element is not present in array")
else:
    print("Element is present at index", result)

3. Time Complexity of Linear Search

From the analysis of the above pseudocode, it can be observed that with the growth of the input list, average and worst-case complexities also grow linearly.

if there are n elements in the list, the worst-case requires n comparisons.

The complexity of linear Search is expressed as T(n) = O(n).

Time Complexity
Worst Case	O(n)
Best Case	O(1)
Average Case	O(n)
Space Complexity
Worst Case	O(1)

4. Advantages of Linear Search

• Linear search can be used irrespective of whether the array is sorted or not. It can be used on arrays of any data type.
• Not require additional memory.
• It is a well-suited algorithm for small datasets.

5. Disadvantages of Linear Search

• Linear search has a time complexity of O(N), which in turn makes it slow for large datasets.
• Not suitable for large arrays.

6. When to use Linear Search?

• When we deal with small datasets
• When we search for a dataset stored in contiguous memory.

FAQs