Recurrence Relations - Step Scribes

Last updated on July 13th, 2024 at 11:09 am

We’ll discuss recurrence relations, recurrence, methods for solving recurrence relations – substitution method, recursion tree method, and master method, and its examples.

1. Recurrence Relations

Recurrence relations are recursive definitions of mathematical functions or sequences.

For example, the recurrence relation defines the famous Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, …:

(1) $\begin{align*} f(x) = f(n-1) + f(n-2) \\ f(1) = 1 \\ f(0) = 1 \\ \end{align*}$

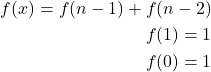
Given a function defined by a recurrence relation, we want to find a `closed form’ of the function. In other words, we would like to eliminate recursion from the function definition.

There are 3 methods to solve recurrence relations:

Substitution method
Recursion-tree Method
Master Theorem

1.1 Recurrences

When an algorithm contains a recursive call to itself, its running time can often be described by a recurrence.

A recurrence is an equation that describes a function in terms of its value on smaller inputs.

For example, the worst-case running time T(n) of the merge-sort can be described as

(2) $\begin{align*} T(n) = \begin{cases} \theta(1) &\text{if } n=0\\ 2T(\frac{n}{2}) + \theta(n) &\text{if } n>1 \end{cases} \end{align*}$

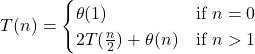
The time complexity of the merge-sort algorithm in the worst-case is $T(n) = \theta (n(log(n)))$

2. Substitution Method

Substitution method consists of guessing an asymptotic (upper or lower) bound on the solution, and trying to prove it by induction.

In other words, using the substitution method, one has to guess the form of the solution.

Consider the recurrence relation : $T(n)=2T( \frac {n}{2})+n$
We guess that the solution is $T(n)=O(n(log n))$ we have to prove that

$T(n) \leq (c(n(log n))) \quad (\therefore c > 0)$

Assume that this bound holds for $\lfloor \frac{n}{2} \rfloor$

$\begin{align*} T(\frac {n}{2}) \leq c(\frac {n}{2}) \cdot log(\frac {n}{2}) + n \\ T(n) \leq 2(c((\frac {n}{2}) log(\frac {n}{2})) + n \\ \leq cn(logn) - cn (log 2) + n \\ \leq cn(logn) - cn + n \\ \leq cn(logn) \quad (\therefore c \ge 1) \end{align*}$

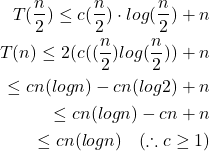
Example : What is the time complexity of the following recurrence relation

(3) $\begin{align*} T(n) = \begin{cases} 1 &\text{if } n=1\\ T(n-1)+n &\text{if } n>1 \end{cases} \end{equation} Solution: \begin{align*} T(n) & = T(n-1)+n \\ & = T(n-2)+(n-1)+n \\ & = T(n-3)+(n-2)+(n-1)+n \\ \vdots \\ & = T(n-(n-1)) + (n-(n-2)) + (n-(n-3)) + ... + (n-2) + (n-1) + n \\ & = T(1) + 2 + 3 + 4 + ... + n \\ & = 1 + 2 + 3 + ... + n \\ & = \frac{n(n+1)}{2} \Rightarrow O(n^2) \\ \end{align*}$

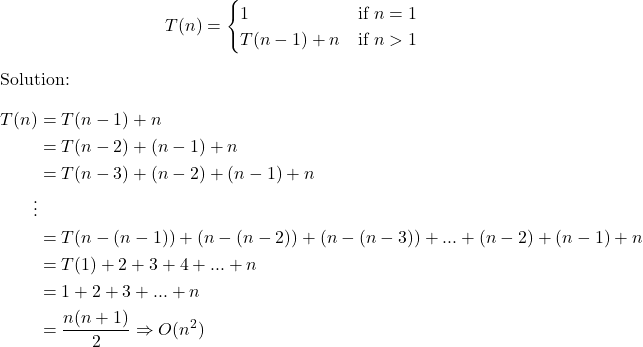
3. Recursion Tree Method

A recursion tree is useful for visualizing what happens when a recurrence is iterated. It represents a tree of recursive calls and the amount of work done at each call is shown with the help of a diagram.

The recursive tree method is good for generating guesses for the substitution method. It can be unreliable and promotes intuition.

In a recursion tree, each node represents the cost of a single sub-problem somewhere in the set of recursive function invocations. We sum the costs within each level of the tree to obtain a set of per-level costs, and then we sum all the per-level costs to determine the total cost of all levels of the recursion.

Recursion trees are useful when the recurrence describes the running time of a divide-and-conquer algorithm.

Example: Consider the recurrence below relation: T(n) = 2T(n\2)+n²

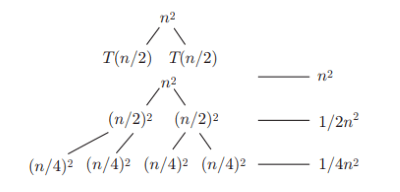
Recursion Tree Method - Recurrence Relations

How deep does the tree go?
We stop at the leaf, and we know we are at a leaf when we have a problem of size 1:

$1 = (\frac {n}{2^i})^2 \Rightarrow n^2 = 2^(2i) \Rightarrow n = 2^i \Rightarrow i = log n$

The amount of work done is given as

$\sum_{i=0}^{log n}{\frac {n^i}{2}} = \Theta n^2$

This is geometrically decreasing in size, so it would not get any bigger than $n^2$ .

4. Master Theorem

Master theorem provides a method to solve various recurrence relations. Although all the relations can’t be solved using this method, it is one of the useful methods of solving complex relations of the form:

$\begin{align*} T(n) = aT (\frac{n}{b}) + f(n) \end{align*}$

where a and b are constants. f is a function of n. this recursive algorithm breaks up the input into sub-problems of size n/b each.

Three cases of master theorem are as follows:

1. If $f(n) = O(n^{log_b (a -\epsilon)})$ for some constant $\epsilon > 0$ , then $T(n) = \theta(n^{log_b (a)})$
2. if $f(n) = \theta(n^{log_b (a)})$ then $T(n) = \theta(n^{(log_b(a))} \cdot log(n))$
3. if $f(n) = \varOmega(n^{log_b (a + \epsilon)})$ for some consant $\epsilon > 0$ and if $af(\frac {n}{b}) \leq cf(n)$ for some constant $c<1$ and all sufficiently large $n$ , then $T(n) = \theta(f(n))$ .

Example: Find the time complexity of the following recurrence relation(using Master Theorem) : T(n) = 5T(n\2)+θ(n²)

Solution:

$\begin{align*} T(n) & = 5T(\frac {n}{2}) + \theta(n^2) \\ & a=5, b=2, f(n)=n^2 \\ \end{align*}$

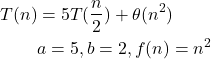
Compare $n^2$ to $n^{log_2 5}$ .
So, time complexity = $O(n^{log_2 5})$ .

FAQs

How to solve recurrence relations?

Three methods to solve recurrence relations:
1. Substitution method
2. Recursion-tree Method
3. Master Theorem

How to solve recurrence relations by using the substitution method?

The substitution method for solving recurrences comprises two steps:
1. Guess the form of the solution.
2. Use mathematical inductions to find the constants and show that the solution works.

Table of Contents