Merge Sort Algorithm

Last updated on July 13th, 2024 at 10:47 am

We will discuss the Merge Sort Algorithm, pseudo code, Code implementation of Merge Sort in C, C++, Java, JavaScript, Python, advantages & disadvantages, and time & space complexity of Merge Sort.

1. What is Merge Sort Algorithm?

Merge Sort is a divide-and-conquer algorithm. It divides the input array into two subarrays, calls itself for the two sub-arrays, and then merges the two sorted arrays.

Merge Sort is a stable sort. It is not an in-place sorting technique.

Merge sort is not preferable for smaller-size element array.

Merge sort is Quick Sort’s complement. This algorithm is used for sorting a linked list.

2. Pseudocode for Merge Sort

The MERGE(A, p, q, r) function is used for merging the two arrays.

The MERGE(A, p, q, r) is a key process that assumes that array[1⋅⋅⋅m] and array[m+1 ⋅⋅⋅ r] are sorted and merges the two sorted sub-arrays into one.

MERGE_SORT(A,p,r)
1. if p < r
2. Then q = floor[(p + r)/2]
3. MERGE (A, p, q) 
4. MERGE (A, q + 1, r) 
5. MERGE (A, p, q, r)

PseudoCode for the MERGE function is given as follows:

MERGE (A, p, q, r) 
1. n1 <- q−p+1 
2. n2 <- r−q
3. create arrays L[1…n1+1] and R[1…n2+1]
4. For i <- 1 to n1
5. doL[i] <- A[p+i−1]
6. For j <- 1 to n2
7. Do R[j] <- A[q +j]
8. L[n1+1] <- ∞
9. R[n2+1] <- ∞
10. i <- 1 
11. j <- 1 
12. For k <- p to r 
13. Do if L[i] ≤ R[j] 
14. then A[k] <- L[i] 
15. i <- i + 1 
16. Else A[k] <- R[j] 
17. j <- j+1

3. Recurrence Relation of Merge Sort

The Recurrence Relation for Merge Sort is

(1)  

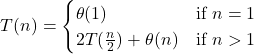
4. Code Implementation of Merge Sort

4.1 Merge Sort in C

#include <stdio.h>
#include <stdlib.h>

// Merge two subarrays of arr[].
// First subarray is arr[l..m].
// Second subarray is arr[m+1..r].
void merge(int arr[], int l, int m, int r) {
    int i, j, k;
    int n1 = m - l + 1;
    int n2 = r - m;

    // Create temporary arrays
    int L[n1], R[n2];

    // Copy data to temporary arrays L[] and R[]
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];

    // Merge the temporary arrays back into arr[l..r]
    i = 0; // Initial index of first subarray
    j = 0; // Initial index of second subarray
    k = l; // Initial index of merged subarray
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // Copy the remaining elements of L[], if any
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    // Copy the remaining elements of R[], if any
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

// l is for left index and r is right index of the
// sub-array of arr to be sorted
void mergeSort(int arr[], int l, int r) {
    if (l < r) {
        // Same as (l+r)/2, but avoids overflow for large l and h
        int m = l + (r - l) / 2;

        // Sort first and second halves
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);

        // Merge the sorted halves
        merge(arr, l, m, r);
    }
}

int main() {
    int arr[] = {54, 26, 93, 17, 77, 31, 44, 55, 20};
    int arr_size = sizeof(arr) / sizeof(arr[0]);

    printf("Given array is \n");
    for (int i = 0; i < arr_size; i++)
        printf("%d ", arr[i]);
    printf("\n");

    mergeSort(arr, 0, arr_size - 1);

    printf("\nSorted array is \n");
    for (int i = 0; i < arr_size; i++)
        printf("%d ", arr[i]);
    printf("\n");
    return 0;
}

4.1.1 Explanation of Merge Sort line by line

• Splitting the array: Merge Sort starts by dividing the array into halves recursively until each sub-array contains only one element.
• Merging: Then it merges the sorted sub-arrays back together. During the merge, it compares elements from both sub-arrays and arranges them in sorted order.
• Combining: This process continues until the entire array is sorted.

4.2 Merge Sort in C++

#include <iostream>
using namespace std;

void merge(int arr[], int l, int m, int r) {
    int n1 = m - l + 1;
    int n2 = r - m;
    
    int L[n1], R[n2];
    
    for (int i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (int j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];
    
    int i = 0, j = 0, k = l;
    
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
    
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
    
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

void mergeSort(int arr[], int l, int r) {
    if (l < r) {
        int m = l + (r - l) / 2;
        
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);
        
        merge(arr, l, m, r);
    }
}

int main() {
    int arr[] = {54, 26, 93, 17, 77, 31, 44, 55, 20};
    int arr_size = sizeof(arr) / sizeof(arr[0]);
    
    cout << "Given array is \n";
    for (int i = 0; i < arr_size; i++)
        cout << arr[i] << " ";
    cout << "\n";
    
    mergeSort(arr, 0, arr_size - 1);
    
    cout << "Sorted array is \n";
    for (int i = 0; i < arr_size; i++)
        cout << arr[i] << " ";
    cout << "\n";
    
    return 0;
}

4.3 Merge Sort in Java

class MergeSort {
    void merge(int arr[], int l, int m, int r) {
        int n1 = m - l + 1;
        int n2 = r - m;

        int L[] = new int[n1];
        int R[] = new int[n2];

        for (int i = 0; i < n1; ++i)
            L[i] = arr[l + i];
        for (int j = 0; j < n2; ++j)
            R[j] = arr[m + 1 + j];

        int i = 0, j = 0;
        int k = l;
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            } else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }

        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }

        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }

    void sort(int arr[], int l, int r) {
        if (l < r) {
            int m = l + (r - l) / 2;

            sort(arr, l, m);
            sort(arr, m + 1, r);

            merge(arr, l, m, r);
        }
    }j


    public static void main(String args[]) {
        int arr[] = {54, 26, 93, 17, 77, 31, 44, 55, 20};
        int arr_size = arr.length;

        System.out.println("Given array is ");
        for (int i = 0; i < arr_size; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();

        MergeSort ob = new MergeSort();
        ob.sort(arr, 0, arr_size - 1);

        System.out.println("Sorted array is ");
        for (int i = 0; i < arr_size; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
}

4.4 Merge Sort in JavaScript

function merge(arr, l, m, r) {
    let n1 = m - l + 1;
    let n2 = r - m;
    let L = new Array(n1);
    let R = new Array(n2);

    for (let i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (let j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];

    let i = 0, j = 0, k = l;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

function mergeSort(arr, l, r) {
    if (l < r) {
        let m = l + Math.floor((r - l) / 2);
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);
        merge(arr, l, m, r);
    }
}

let arr = [54, 26, 93, 17, 77, 31, 44, 55, 20];
console.log("Given array is ");
console.log(arr.join(" "));
mergeSort(arr, 0, arr.length - 1);
console.log("Sorted array is ");
console.log(arr.join(" "));

4.5 Merge Sort in Python

def merge(arr, l, m, r):
    n1 = m - l + 1
    n2 = r - m

    L = [0] * (n1)
    R = [0] * (n2)

    for i in range(0, n1):
        L[i] = arr[l + i]

    for j in range(0, n2):
        R[j] = arr[m + 1 + j]

    i = 0
    j = 0
    k = l

    while i < n1 and j < n2:
        if L[i] <= R[j]:
            arr[k] = L[i]
            i += 1
        else:
            arr[k] = R[j]
            j += 1
        k += 1

    while i < n1:
        arr[k] = L[i]
        i += 1
        k += 1

    while j < n2:
        arr[k] = R[j]
        j += 1
        k += 1

def mergeSort(arr, l, r):
    if l < r:
        m = (l+(r-1))//2
        mergeSort(arr, l, m)
        mergeSort(arr, m + 1, r)
        merge(arr, l, m, r)

arr = [54, 26, 93, 17, 77, 31, 44, 55, 20]
print("Given array is", arr)
mergeSort(arr, 0, len(arr)-1)
print("Sorted array is", arr)

5. Advantages of Merge Sort

1. It guarantees a worst-case time complexity of O(n log n), where n is the number of elements.
2. Stable sorting algorithm, meaning it preserves the relative order of equal elements.
3. Performs well on large data sets and is efficient for sorting linked lists.

6. Disadvantages of Merge Sort

1. Requires additional memory space for the merging process, which can be a disadvantage for large arrays or in memory-constrained environments.
2. It is slower than other sorting algorithms for small data sets or arrays that can fit entirely in memory.

7. Time and Space Complexity of Merge Sort

Time Complexity
Worst Case	O(n log n)
Best Case	O(n log n)
Average Case	O(n log n)
Space Complexity
Worst Case	O(n)

8. Applications of Merge Sort

• Merge sort is useful for sorting linked lists in O(n log n) time. Other (n log n) algorithms such as heap sort and quick sort (average case n log n) cannot be applied to linked lists.
• It is used in the inversion count problem.
• It is used in external sorting.

FAQs